Como detectar distorções no Ibovespa com a Lei de Benford no Python

A Lei de Benford é conhecida como a Lei do Primeiro Dígito Significativo. É uma teoria sobre a distribuição de probabilidade do primeiro dígito de cada número de um conjunto aleatório de dados. O que isso significa?

Se perguntarmos qual é a probabilidade do número 9 ser o dígito mais significativo de um número qualquer, podemos automaticamente pensar que é 11% (1 possibilidade em 9 dígitos possíveis, considerando que o primeiro dígito significativo de um número positivo é o dígito não nulo mais à esquerda em sua representação decimal). Não é bem assim pela Lei de Benford. Segundo ela, a distribuição dos primeiros dígitos significativos é dada por 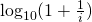, ou seja,

Fonte: http://www.isaca.org/Journal/Past-Issues/2011/Volume-3/PublishingImages/11v3-understanding-and.jpg

Onde esta teoria é utilizada?

Acredite você ou não, ele foi utilizada para detectar a fraude nas eleições iranianas de 2009 e é aceita como evidência em um processo criminal em diversos estados dos EUA. Uma outra aplicação, objetivo do post de hoje, é detectar pertubações no mercado de ações. Como?

Imagine se os preços das ações listadas no IBovespa seguissem a Lei de Benford? Se plotarmos a distribuição do primeiro dígito do preço cada um dos papéis que compõe o índice, temos o seguinte gráfico:

Próximo o suficiente? Podemos testar estatisticamente se esta distribuição do IBoveps segue a de Benford com um teste Chi-Quadrado. Neste caso, calculado os desvios, considerando 5% de erro e 8 graus de liberdade, ao olharmos na tabela temos que conjunto de dados satisfará a Lei de Benford se chi^2 < 15.51

De fato, para este nosso conjunto, temos 9,97. Assim, concluímos que a distribuição dos primeiro dígitos dos preços das ações seguem a Lei de Benford. Preços de fechamento de 08.05.2014

Mas, qual é aplicação disso?

Dado que a distribuição ibov "obedece" (o mercado é soberano) à Benford, podemos tentar detectar desvios nos preços e identificar pontos de compra e venda dos papéis. Estudos indicam que o mercado está super avaliado quando a quantidade de 1s como primeiro dígito é maior que a na Lei de Benford. Na tabela abaixo, tem-se um exemplo da mesma aplicação, só que para o STI components da bolsa dos EUA.

Fonte: http://dev.bigfatpurse.com/wp-content/uploads/Benford-Compare.png

Observe que, na crise em 2008, a distribuição do STI possui uma dispersão muito elevada, indicando que o mercado estava "barato".

E o Python?

Hoje trazemos um código em Python que calcula a Lei de Benford para dois conjuntos de dados: os preços de fechamento de 08.05.2014 e a variação absoluta em 12 meses dos papéis, também no mesmo dia. Acesse o código no Git: https://github.com/leandrowar/ArtWithDataCodes

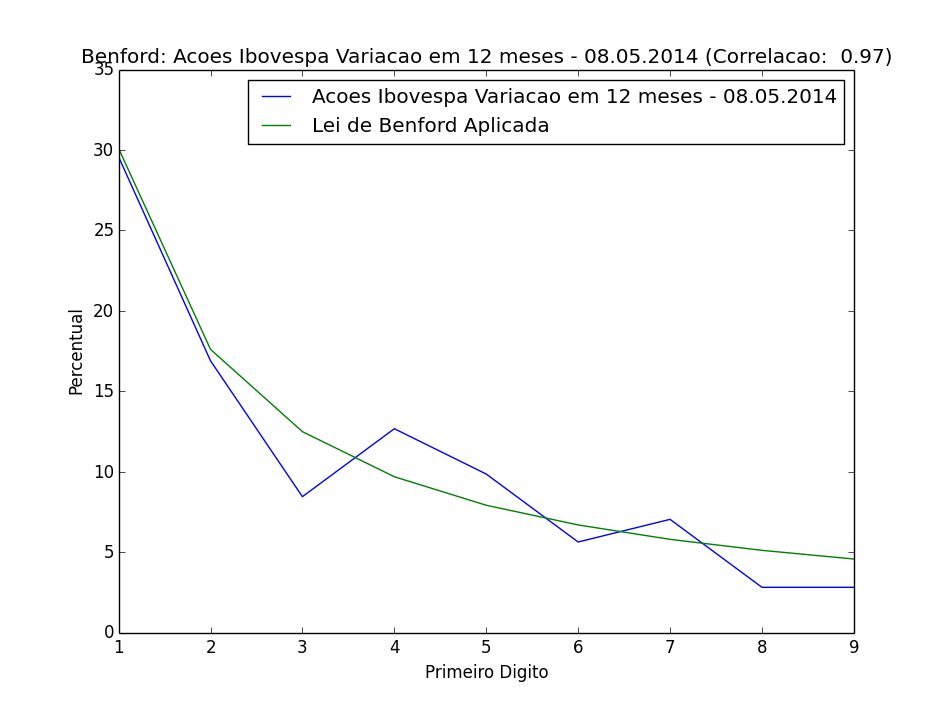
No gráfico abaixo, temos a distribuição da variação dos últimos 12 meses. Temos alguma distorção mais acentuada nos dígitos 3 e 4, indicando que talvez possam ser o momento de comprar os papéis do dígito 3 e vender os papéis do dígito 4. O teste do chi^2 revela que esta distribuição não segue a Lei de Benford, reforçando a teoria de distorção no mercado. Mas, testes com bases de dados maiores ainda são necessários, antes de qualquer conclusão. Nosso foco ainda está no estudo aplicado do Python.

Um abraço e até o próximo post!